Rangkuman Materi matematika kelas 10 bab 7 Kurikulum Merdeka
Bismillah, apa kabar bapak/ibu guru matematika kelas X yang kami banggakan. Semoga anda senantiasa dalam keadaan sehat walafiat. Baiklah menjelang pembelajaran ganjil dan genap bulan januari tahun 2022/2023, pada kesempatan baik ini ini guru-id berbagi rangkuman materi pelajaran bahasa inggris kelas sepuluh SMP/MTS yang terdiri dari 8 (delapan) bab pada kurikulum merdeka. nah pada kesempatan ini guru-id akan berbagai materi bab 7 statistika, selanjutnya Bagi teman-teman guru yang membutuhkan referensi silahkan simak portingan ini hingga akhir.
Rangkuman materi matematika kelas X bab 7
Berikut rangkuman materi bab tujuh statistika yang merupakan pembelajaran pada semester genap kurikulum merdeka
Statistik adalah ilmu yang akan membantu kalian menguasai berbagai hal yang terkait dengan data, mulai dari pengumpulan data, mengolahnya, menganalisis sampai akhirnya mengambil keputusan berdasarkan data
1. Diagram lingkaran sederhana atau diagram batang sederhana dapat digunakan untuk menampilkan informasi yang tersedia, baik dalam bentuk data tunggal maupun dalam bentuk tabel frekuensi.
2. Dari data tunggal sederhana atau data dalam tabel distribusi frekuensi, bisa diperoleh ukuran pemusatan: mean, modus, dan median yang dapat memberikan gambaran tentang kumpulan data tersebut.
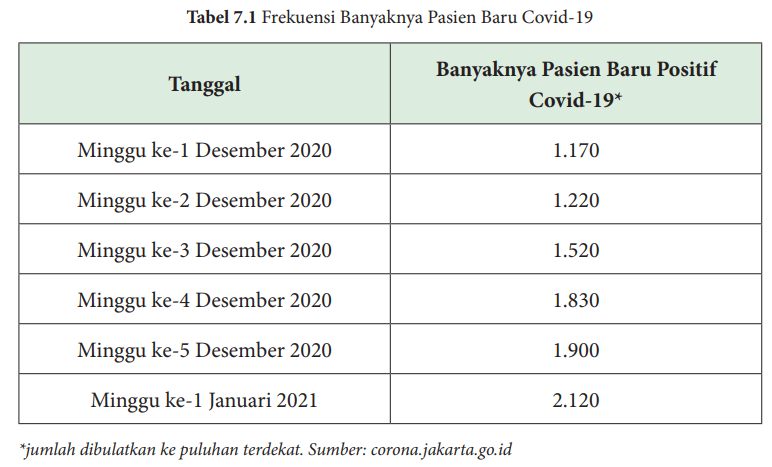
Penggunaan Diagram Batang untuk Menganalisis DataPandemi Covid-19 melanda seluruh dunia. Setiap harinya jumlah pasien yang terinfeksi virus Covid-19 terus bertambah. Pada tabel berikut, kalian dapat melihat rata-rata pertambahan pasien baru positif Covid-19 setiap minggunya di Provinsi DKI Jakarta
1. Dari Tabel 7.1 di atas, pada minggu ke berapakah yang mengalami rata-rata kenaikan jumlah pasien positif Covid-19 yang paling besar?
2. Jika pola penambahan rata-rata mingguan jumlah pasien positif Covid-19 ini terus bertambah, berikan estimasimu untuk jumlah pasien positif Covid-19 pada minggu ke-2 Januari 2021. Jelaskan alasanmu!
3. Saat menentukan kenaikan jumlah pasien Covid-19 yang paling besar, manakah yang lebih mudah digunakan, tabel atau diagram batang? Jelaskan!
A. HistogramAda berbagai tipe diagram. Diagram mana yang paling baik untuk digunakan sangat tergantung pada data apa yang kalian miliki dan informasi apa yang ingin kalian sampaikan.
Salah satu diagram yang dapat kalian gunakan adalah histogram. Histogram hampir serupa dengan diagram batang, namun histogram berbeda dengan diagram batang. Gambar 7.1 dan 7.2 menunjukkan contoh histogram dan diagram batang.
Histogram biasanya digunakan untuk menunjukkan distribusi dari suatu kelompok data, sedangkan diagram batang digunakan untuk membandingkan data. Histogram menampilkan data yang sifatnya kuantitatif dengan rentang data yang dikelompokkan ke dalam interval, sedangkan diagram batang menampilkan data yang sifatnya kategori.
Perbedaan lainnya, pada histogram, gambar batang menempel satu sama lain, sedangkan pada diagram batang, ada spasi antarbatang. Perbedaan terakhir, diagram batang biasanya memiliki batang dengan lebar yang sama, sedangkan lebar batang dalam histogram tidak perlu sama selama luas totalnya seratus persen jika digunakan persen atau luas total sama dengan jumlah data. Oleh karena itu, frekuensi data dalam diagram batang dilihat dari panjang batang, sedangkan frekuensi dalam histogram diberikan berdasarkan area pada masing-masing batang.
Perhatikan Gambar 7.3. Kedua histogram menampilkan data yang sama. Cobalah mencari bagaimana kedua histogram ini menjelaskan data yang sama walaupun terlihat berbeda.
Pada histogram sebelah kiri:• Frekuensi Kelas 0-2 adalah 8, luas persegi panjangnya adalah 2 × 8 = 16
• Frekuensi Kelas 2-4 adalah 16, luas persegi panjangnya adalah 2 × 16 = 32
• Luas gabungan kedua kelas tersebut adalah 16 + 32 = 48
Pada histogram sebelah kanan:• Frekuensi Kelas 0-4 adalah 12, luas persegi panjangnya adalah 4 × 12 = 48 Jadi, kelas 0-2 dan 2-4 pada histogram kiri memiliki luas yang sama dengan kelas 2-4 pada histogram kanan, sehingga dapat dikatakan bahwa histogram kiri dan histogram kanan menjelaskan data yang sama
Frekuensi RelatifFrekuensi pada histogram tidak harus selalu menunjukkan banyaknya data yang ada dalam setiap interval. Histogram juga dapat menggunakan persentase sebagai frekuensi relatif dari setiap kelas intervalnya.
Dari histogram pada Gambar 7.5, ditunjukkan bahwa ada 16% siswa yang mendapatkan nilai matematika antara 70 sampai 75.
• Apakah ini berarti ada 16 siswa yang berada di kelas tersebut? Jelaskan!
• Interval kelas manakah yang memiliki persentase terbesar? Berapa persen kelas dengan interval tersebut?
Misalkan ada 200 siswa yang mengikuti ulangan matematika tersebut. Berapakah banyaknya siswa yang mendapatkan nilai 85 ke atas tapi di bawah 90?
Apabila kalian menambahkan seluruh persen pada setiap interval, berapakah seharusnya jumlah total persen yang kalian peroleh? Jelaskan!
Histogram dengan frekuensi relatif sangat efektif jika digunakan untuk membandingkan dua kelompok data dengan jumlah data yang berbeda, misalnya, jika kalian ingin membandingkan data harian berapa persen penduduk di Jakarta dengan penduduk di Bali yang telah sembuh dari Covid-19. Karena jumlah total penduduk yang terinfeksi Covid-19 di Jakarta berbeda dengan Bali, maka penggunaan persentase sebagai frekuensi relatif memberikan gambaran yang lebih baik.
Modus dan Median
Modus dan median adalah dua ukuran pemusatan untuk melihat kecenderungan kumpulan data.
Median adalah nilai data yang berada tepat di tengah ketika seluruh data diurutkan dari yang terkecil sampai yang terbesar. Untuk mencari letak median, bagilah banyaknya data dengan 2.
• Jika hasilnya adalah bilangan bulat, m, maka median terletak di tengah-tengah antara urutan ke-m dan ke-(m + 1).
• Jika hasil baginya bukan merupakan bilangan bulat, bulatkanlah hasilnya ke atas, maka median terletak di urutan sesuai hasil pembulatan.
Modus dari sebuah kumpulan data adalah data yang paling sering muncul atau memiliki frekuensi paling besar. Kedua ukuran pemusatan ini memiliki keuntungan, yaitu tidak terpengaruh jika kumpulan data memiliki data pencilan atau data yang berbeda dari kumpulan datanya.
Selain modus dan median, kalian bisa melihat rentang dari kumpulan data melalui range atau jangkauan. Jangkauan adalah selisih antara data terkecil dengan data terbesar.
Mean (Rerata atau Rata-Rata)
Rerata atau mean adalah ukuran pemusatan lain selain median dan modus. Mean dari sebuah kumpulan data adalah bilangan yang diperoleh dengan mendistribusikan secara merata ke seluruh anggota dari kumpulan data. Kalian bisa menghitung mean dengan cara menambahkan seluruh nilai data dan membagi dengan total banyaknya data
Mean/Rata-Rata Data Kelompok
Data penjualan sepatu di toko A pada Tabel 7.4 merupakan kumpulan data tunggal. Kalian dapat mengelompokkan data-data ini menjadi data kelompok dengan panjang kelas sama dengan 2 sehingga menjadi tabel frekuensi data kelompok sebagai berikut.
Cara menghitung rata-rata dari data kelompok di atas adalah menggunakan nilai tengah dari tiap kelompok. Data tunggal dalam kelompok diasumsikan tersebar secara merata, sehingga nilai tengah dari setiap kelompok dapat diasumsikan mewakili kelompok tersebut.
Nilai tengah kelompok 37-39 adalah 38, Nilai tengah kelompok 40-42 adalah 41, Nilai tengah kelompok 43-45 adalah 44, dan Nilai tengah kelompok 46-48 adalah 47. Rata-rata dari kelompok di atas:
Latihan 7.41. Secara geografis Indonesia dilalui oleh garis khatulistiwa sehingga hanya terdapat 2 musim, yaitu musim panas dan musim hujan. Oleh karena itu, sangat penting bagi kita untuk memahami faktor penting apa saja yang ada pada kedua musim tersebut agar kita dapat mempersiapkan diri dengan lebih baik dalam usaha hidup berdamai dengan alam. Salah satu faktor yang penting yang menentukan musim adalah faktor curah hujan.
Curah hujan adalah jumlah air hujan yang turun pada suatu daerah dalam kurun waktu tertentu. Dengan kata lain, curah hujan adalah volume air hujan yang terkumpul dalam bidang datar dalam periode tertentu.
Biasanya curah hujan dinyatakan dalam satuan milimeter. Data curah hujan yang ditampilkan adalah ketinggian air hujan yang terkumpul di tempat datar seluas 1 meter persegi. Jadi, jika curah hujan sebesar 1 mm artinya volume air hujan yang terkumpul pada tempat datar seluas 1 meter persegi ada sebanyak 1 liter. Pada umumnya curah hujan dikategorikan menjadi 3 kategori, yaitu rendah (0-100 mm), menengah (100-300 mm) dan tinggi (300-500 mm).
Perhatikan data curah hujan di Kota Samarinda sepanjang tahun 2017 berikut (dalam mm, dibulatkan ke satuan terdekat):
161 139 88 343 309 421 161 250 100 152 219 223
a. Tentukanlah median dari data tersebut.
b. Tentukanlah Q₁ dan Q₃ dari data tersebut. Apakah kalian perlu melakukan interpolasi?
LEBIH LENGKAP: